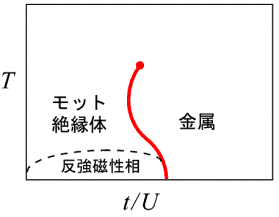
電子相関(特に短距離のクーロン斥力)が強いことを主因として、電子濃度が単位格子あたりちょうど奇数となっているときに生じる絶縁体はモット絶縁体として知られている。モット絶縁体に対して、電子濃度を奇数からずらしたり(キャリアドーピング)、あるいはクーロン斥力の大きさに対してバンド幅を増大させる(バンド幅制御)ことにより金属や超伝導への金属絶縁体転移を引き起こすことができる。これはモット転移と総称される。モット転移は熱力学的な相転移であるが、その本性は何十年にもわたって未解明であった。困難の原因には、モット転移が電子状態を根本的に変えてしまうために波及効果が大きくて、他の自由度の相転移を同時に伴うことも多く、モット転移だけを純粋に取り出して初めて見える本質を見極めるのが難しかったことなどがある。

しかし、上図の典型例に見られるように、クーロン斥力に対するバンド幅(上図の横軸t /U )を制御して生じるモット転移では、温度Tを変えて得られる有限温度相図内の赤い線で表される一次相転移の相境界のように、低温で生じる反強磁性相(AF)などへの相転移に邪魔されずにモット転移だけを取り出すことができる場合がある。低温からこの赤い相境界を辿っていくと赤丸で示されている臨界点に達する。モット絶縁体はそれ自身としては対称性の破れを伴っていないので、有限温度では臨界温度以上の温度を経由してモット絶縁体相から金属相に連続的に(断熱的に)回り込むことができる。このような事情が下左図のような液体と気体の間の相転移(気相液相転移)のときに似ていることに読者も気づかれるであろう。
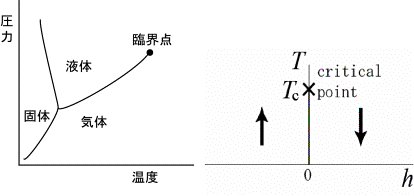
気相液相転移の場合には上右図に示されている磁場( h ) 中でのイジング模型の相転移(磁場下向き(h>0) のためにスピンが下向きに揃う相からh<0のためにスピンが上向きに揃う相への一次転移)と同型であることが知られている。ではモット転移の臨界点ではどうなっているのかという疑問が当然生じるが、この特定には長い年月を要した。 Limeletteら[1] は2003年にV2O3のモット転移の450K付近の臨界温度近傍で、電気伝導度の特異性から、確かにイジング模型と同じ臨界指数が得られることを示した。今の場合の臨界指数は、圧力pを変化させたときの伝導度σの臨界値σcから測った特異性 | σ-σc|∝|p -pc|1/δで決まるδや、臨界温度以下での1次転移での伝導度のとびΔσ∝|T - Tclβから決まるβ、感受率の発散の仕方を決めるγ(すなわちd σ/dp ∝|T- Tc| γから決まるγ)などがある。Limelette らは臨界指数が 3次元イジング模型で知られている厳密な値β~ 0.32, δ~ 4.8などで矛盾なく説明できることを示したのである。
ところで、イジング模型の場合は横磁場をかけるとスピン上向きの状態と下向きの状態との間の量子トンネリングが誘起され、この量子ゆらぎのために転移温度が下がる。モット転移のときにも何らかの方法で量子効果を増大させて、モット転移の臨界温度が低くしたらどうなるであろうか?特に臨界温度が絶対零度になったときは量子臨界現象が生じるはずであるが、このとき転移の様相はどうなると予想されるだろうか?この量子相転移の問題は量子モンテカルロ計算などの理論計算が行なわれた結果、イジング模型の相転移とは全く異なる新奇な臨界現象とスケーリング則が予想された[2]。特に最近の我々のグループの理論研究は、この考察をさらに進め、イジング模型も従う標準的な相転移の枠組みであるギンツブルグ・ランダウ・ウィルソン型の相転移とは異なる、新しいタイプの相転移がモット転移の普遍性クラスとして導かれた[3-6] 。この普遍性クラスではゆらぎの効果が重要でなくなる上部臨界次元であるにもかかわらず、β = d/2, δ = 4/d, γ = 2 -d l /2 のように系の空間次元に依存する大変異常な臨界指数が得られる。
相転移が生じる機構には 2つのものが知られている。その一つがランダウの指摘した自発的対称性の破れを伴う相転移であり、もう一つがリフシッツの指摘したトポロジーの変化に伴って生じる相転移である。前者の典型は強磁性や反強磁性転移、超伝導転移などであり、後者はフェルミ面のトポロジーの変化によって生じるリフシッツ転移や、相互作用のない電子系で生じるバンド絶縁体と金属の間の転移である。この2 種の相転移は、従来全く異なる機構で生じ、互いに関連はないものと信じられてきた。ところが、モット転移で得られた、新しい普遍性クラスに属する相転移はこの2種類の相転移の間に深いつながりがあることを示すものである。
一方、賀川、宮川、鹿野田は擬2次元的な有機導体κ -(BEDT-TTF)2Cu[N(CN)2]Clに生じる 40K付近のモット臨界点に注目した。詳細かつ徹底した実験により電気伝導度の特異性を調べ、β ~ 1, δ ~ 2, γ ~ 1 という値を得た[7] 。この値は、どんな空間次元のイジング模型の臨界指数とも一致しないし、その他のよく知られている模型の臨界指数とも一致しない。また上述のV2O3 の結果と異なる結果である。一方この一連の指数は上に述べた量子モット転移で空間次元d = 2とおいて期待される値と一致し、通常のスケーリング則を満たす。
モット転移の研究の歴史が70年近くにおよぶにもかかわらず、この相転移や臨界現象の性格が実験的に定量的な評価の対象となってきたのはわずかここ数年のことでることに驚くかもしれない。一方この転移がイジング模型や気相液相転移の普遍性と一致したり、多くの相転移の満足するギンツブルグ・ランダウ・ウィルソンの枠組みに従わなかったりして、基礎物理学的に見て新しい概念を生み出す舞台であることもはっきりしてきた。一連の研究から明らかとなってきたこともまたびっくりするような出来事の連続である。モット転移や相関絶縁体からの転移はもともとのギャップが eVのオーダーの大きさに及ぶ場合もあるから大変エネルギースケールの大きな相転移である。この相転移の近傍には銅酸化物に見られる高温超伝導をはじめとして、未解明の現象が多く見出される。この機構を解明するためにはモット転移それ自身の機構と本質の解明が必須であることは、銅酸化物超伝導発見以来繰り返し強調されてきた。このモット転移のメカニズムがようやくわかりかけてきているといえる。モット転移の臨界性の異常さが未解明のドラマティックな現象を生み出す根底にあると予想される。
[1] P. Limelette et al.: Science 302 (2003) 89.
[2] M. Imada: J. Phys.Soc. Jpn. 64 (1995) 2954.
[3] M. Imada: J. Phys.Soc. Jpn. 74 (2005) 859.
[4] M. Imada: Phys. Rev.B 72 (2005) 075113.
[5] T. Misawa, Y. Yamaji and M. Imada: J. Phys. Soc. Jpn. 75 (2006) 083705.
[6] T. Misawa and M. Imada: Phys. Rev. B 75 (2007) 115121.
[7] F. Kagawa, K. Miyagawa and K. Kanoda: Nature 436 (2005) 534.