 この章の最初にもどる
この章の最初にもどる  次のページ
次のページ![]()
─なぜ量子系でモンテカルロ法を使うの?
|
|
|
|
すなわち

しかし

そこで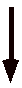


| 相互作用のない量子系: |
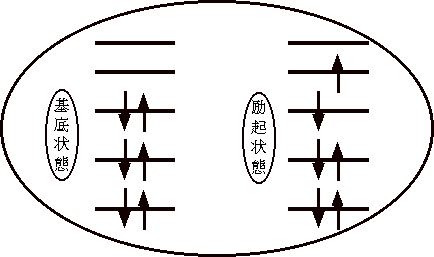
問題なのは
| 相互作用している多体量子系: |
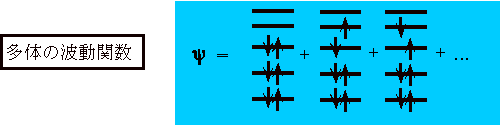
数値計算を行なううえで、厳密な答えを得ようとすると小さなサイズのクラスターしか扱えない。 例えば電子系の場合は、厳密に
この時も困難がある。多くの一粒子状態を同時に取り扱わなければならなくなる
という点である。重ね合わせなければならない一粒子状態の数は系の大きさの
指数関数に比例する。このため系の大きさを増やすにしたがい取り扱う状態の
数が指数関数的に増大して計算機の能力をすぐに超えてしまう。
![]()
取り扱おうとすると現在の計算
機の能力では20個程度の電子
を取り扱うのが限界となってい
る。 


| フェルミオン系のモンテカルロ法としては |

(変分モンテカルロ法
また関係の深い計算手法として数値的な密度行列くりこみ群
量子モンテカルロ法は動的平均場近似