＊古典系では初期状態を決めればそれ以降の運動の経路は一意的に決定される。
　ニュートンの運動方程式を解けば良い。

数値計算を行なうためには時間軸を離散化して、下図のように曲線の経路を細かく分けた折れ線に置き換えることが多い。

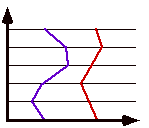各時刻 t ごとに、粒子の座標x1(t), x2(t),...それぞれについてサンプル和をとれば量子ゆらぎの効果をとり入れることができる。つまり上図のような経路（折れ線）のいろいろな形についてサンプル和をとることになる。

　ハバード模型（B-2-2）や量子スピン模型（B-2-1）のような格子上の理論模型ではラグランジアンを局所的に分解することにより、効率よく和をとることができる。これをチェッカーボード法（チェッカーボード分解）と呼び下図のような経路和を行なう。

粒子の運動と実時間変化を追いかけるためにはexp[iHt]（ここでHは系のハミルトニアン、tは時間）という演算子をとりあつかう必要がある。なぜなら量子力学的状態|ψ＞の時間変化はexp[iHt]を作用させたexp[iHt]|ψ＞によって与えられるからである。しかし、この場合複素数を扱わなければならなくなる。一方モンテカルロ法の確率分布関数は実数の正定置でなければならないため、これらの間に関係をつけるには特別の工夫を要する。

　一方、統計力学平均を求める時にはアンサンブル平均をとる。これは分配関数

　　　
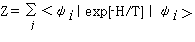
を計算すると実行できる。ここでＴは温度、iについての和はすべての量子力学的状態についての和である。

この章の最初にもどる

次のページ

今田研究室ホームページへ